Re: 2010電気計算9月号　2種2次変電 - 電験三世

2010/09/18 (Sat) 17:31:26
*.bbexcite.jp

　マサさん　こんにちは。

　電圧降下の簡易式の両辺に、Ｖrをかけると、

　Vr^2=Vs*Vr-(R*P+X*Q)

となります。ここで、両辺を基準電圧Ｖbで割ると、

　Vr(p.u.)*Vr=Vs(p.u.)*Vr-(R*P+X*Q)/Vb

さらに、両辺をＶrで割ると、

　Vr(p.u.)=Vs(p.u.)-(R*P+X*Q)/(Vb*Vr)

解答では、有効分の要素を無視しているので、

　Vr(p.u.)=Vs(p.u.)-X*Q/(Vb*Vr)

となります。
　Ｘ*Ｑの単位は［Ｖ^2］なので、右辺２項は、無単位。
　単位法で表したVr(p.u.)、Vs(p.u.)も無単位。
　ですから、単位法で計算する上では、式が成り立つ。
　と、以上のように考えてみました。

　ちなみに、コンデンサを設置しない場合の解答を、ＵＰしてみました（私のいつもの解き方です）。
　間違っていたら、すみません。

Re: 2010電気計算9月号　2種2次変電 - 鹿の骨

2010/09/18 (Sat) 18:35:05
*.dti.ne.jp

こんばんは

この問題は電圧降下の式をVr=Vs-√3I*(Rcosθ+Xsinθ)で解いています。

スレ主さんの疑問で
「ﾘｱｸﾀﾝｽと無効電力を掛けたものが電圧[V]と同単位になるのでしょうか？」
は、なりません。

単位法で計算していますので、単位法で表した無効電力と同じく単位法で表した無効電流が同じpu値になるのが要です。
電圧降下△Ｖは
△Ｖ[pu]＝電流[pu]・Ｘ[pu]・sinθ
ですが、
△Ｖ[pu]＝電流[pu]・sinθ・Ｘ[pu]＝無効電流[pu]・Ｘ[pu]＝Ｑ[pu]・Ｘ[pu]
となります。

尚、この問題はオーム法で解くと解りますが、この計算は成立しないと思います。
瑕疵がある問題だと思います。
負荷電流を定格電圧時の値で計算していますが、実際には二次電圧は定格電圧ではありません。
電流値の計算は相当に厄介な方程式を解かないと出てきません。

Re: 2010電気計算9月号　2種2次変電 - fukusima

2010/09/18 (Sat) 20:40:54
*.bbtec.net

こんばんは、マサさん

電圧降下の近似式　⊿V＝Vs－Vr＝√3I*(Rcosθ+Xsinθ)　〔V〕･････①
受電端の有効電力P3r､無効電力Q3rは
P3r＝√3VrIcosθ　〔W〕
Q3r＝√3VrIsinθ　〔var〕
①式の右辺にVr/Vrを掛けると
＝√3I*(Rcosθ+Xsinθ)×Vr/Vr
＝(√3IVrcosθ･R＋√3IVrsinθ･X)/Vr
＝P3r･R/Vr＋Q3r･X/Vr　〔V〕
この問題ではR=0であるので、
⊿V＝Vs－Vr＝Q3r･X/Vr
∴Vr＝Vs－Q3r･X/Vr　となる。

「電圧降下を求めるのに、ﾘｱｸﾀﾝｽと無効電力を掛けたものが電圧[V]と同単位になるのでしょうか？」
解答ではX12'･Qtになっている部分はX12'･Qt/V2(p.u.)になると考えられます。（電圧[V]と同単位になる）
したがって解答ではなぜX12'･Qtとなっているのか疑問です。（理解できません！！）

この予想問題は平成９年度の電力･管理問題と非常に良く似てます。
私の持っている参考書では近似式を使った場合と使わない場合についての計算結果があります。
近似式を使った場合の計算結果は　V2(p.u.)＝0.8627(p.u.)
近似式を使わない場合の計算結果は「電験三世さん」と同じ結果になってます。V2(p.u.)＝0.8492(p.u.)

Re: 2010電気計算9月号　2種2次変電 - ﾏｻ

2010/09/18 (Sat) 22:00:54
*.so-net.ne.jp

こんばんわ

電験三世さん、鹿の骨さん、ありがとうございました。
単位が同じになるかに注目して考えていましたが、そもそも単位法[p.u.]で表すと無単位であり、また単位法で表す事で無効電流[p.u.]と無効電力[p.u.]が等しくなるというのがポイントだと判りました。
ｵｰﾑ法で解こうとすると確かに厄介ですが、電力管理においてこの種の問題（変圧器の電圧降下を求める問題）では、単位法により解答の様な方法で解くのがﾍﾞｽﾄなのでしょうか？

Re: 2010電気計算9月号　2種2次変電 - ﾏｻ

2010/09/18 (Sat) 22:17:18
*.so-net.ne.jp

fukushimaさん、こんばんわ。投稿画面をしばらく開いたまま所用で離れていましたので、レスを確認する前に投稿してしまいました。
もしお手数でなければ、その平成9年度の問題を添付頂ければ幸いです。私の持っている過去問題は平成11年度までです･･･その問題を自身で解いてみたいと思います。よろしくお願いいたします。

Re: 2010電気計算9月号　2種2次変電 - 鹿の骨

2010/09/18 (Sat) 22:41:59
*.dti.ne.jp

この問題の解法がインチキ臭いと思うところは負荷電流の計算が定格電圧を前提に計算されているところです。
これは単位法で計算してもオーム法で計算しても同じ事で、変圧器の二次電圧はこの問題の場合「不明」です。
従って負荷電流はそう簡単には出てきません。
「単位法で計算する場合は定格電圧と見なして計算して良い。」と言う事は断じてありません。

Re: 2010電気計算9月号　2種2次変電 - 素敵なおじさん

2010/09/18 (Sat) 23:06:46
*.dti.ne.jp

鹿ちゃんのいいたいことはわからないでもないが
66ｋVの変電所の負荷として80MW0.8と書いてあるのだから素直に66ｋVで負荷を計算すれば良いのではないだろうか？
もし定格電圧が仮定できないとすれば負荷のMW表記は成立しないことになるな

Re: 2010電気計算9月号　2種2次変電 - 鹿の骨

2010/09/19 (Sun) 00:19:52
*.dti.ne.jp

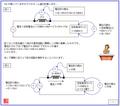こういう事になると思います。

変圧器二次側の電圧を66kVと見なして計算して良いのなら問題そのものが成立しません。
二次側母線の電圧は幾つか・・・66kVです！
アホカ！

Re: 2010電気計算9月号　2種2次変電 - 素敵なおじさん

2010/09/19 (Sun) 10:44:39
*.dti.ne.jp

負荷が一定でコンデンサを増やしたときの母線電圧はどうなるか？という問題だから元の母線電圧が66ｋVと見なして計算すれば良いと思うけど？
式で書くと
電圧降下は　V≒IwR＋IrX から 電圧降下⊿Vは
⊿V＝(Ir0-Ir)X＝IcX　IwRは相殺される　
Ir0：　初期の無効電流
Ir：　コンデンサ接続による無効電流の減少分
Ic：　コンデンサ接続後の無効電流

Re: 2010電気計算9月号　2種2次変電 - 通りすがり

2010/09/19 (Sun) 13:12:57
*.asahi-net.or.jp

単位法ってどんなにして計算するんだったけ？！
短絡容量の計算なら得意なのに！　ホントはウソ！

まてよ！　
変圧器容量と％Ｚが分かっているので短絡容量が計算出来るぞ！
６６ｋＶ母線側の短絡容量は
１００ＭＶＡ÷１６％×（１５０／１５４）＝６０８．７ＭＶＡ　計算あってるかな？
コンデンサーを投入する事で電圧が上昇する割合は
コンデンサー容量÷短絡容量だったはず
１０ＭＶＡ÷６０８．７ＭＶＡ×１００＝１．６４（％）
これで合ってるかな？　珍回答でした。

Re: 2010電気計算9月号　2種2次変電 - Y-Delta

2010/09/20 (Mon) 08:39:02
*.ocn.ne.jp

>>１００ＭＶＡ÷１６％×（１５０／１５４）＝６０８．７ＭＶＡ　計算あってるかな？

合っていないと思う。

Re: 2010電気計算9月号　2種2次変電 - 通りすがり

2010/09/20 (Mon) 11:55:07
*.asahi-net.or.jp

やっぱり間違ってますか！
電圧を２乗しないといけないかな
１００ＭＶＡ÷１６％×（１５０／１５４）×（１５０／１５４）＝５９３ＭＶＡ
これで計算すると、
１０ＭＶＡ÷５９３ＭＶＡ×１００＝１．６８６（％）
これも違ってるかも？？　

Re: 2010電気計算9月号　2種2次変電 - fukusima

2010/09/21 (Tue) 00:34:52
*.bbtec.net

マサさん、こんばんは！！

平成９年度の問題は次の２点が違っているだけです。
1.変圧器の二次側にコンデンサ１０〔Mvar〕が２０〔Mvar〕
2.使用タップ:二次側６６〔kV〕が７７〔kV〕
解答方法は電験三世さんの添付ファイルの解答方法と同じです。

＜電圧降下の近似式を使わない場合、以下の関係式が成り立つ＞
Vs^2＝{Vr＋(P3r･R＋Q3r･X)/Vr}^2＋{(-Q3r･R＋P3r･X)/Vr}^2
を使用して解答してます。

Re: 2010電気計算9月号　2種2次変電 - 受験生

2010/09/22 (Wed) 19:36:00
*.ocn.ne.jp

電験三世　様

皆様いつも大変お世話になります。

『コンデンサを設置しない場合』の計算式のＵＰ大変に参考になりました。

『コンデンサを設置した場合』の計算式をＵＰしていただけないでしょうか？

宜しく御願いいたします。

Re: 2010電気計算9月号　2種2次変電 - ﾏｻ

2010/09/24 (Fri) 00:19:26
*.spmode.ne.jp

たくさんレス頂き、ありがとうございました。
本問題において、たまたま本屋でテキストの立ち読みをしていると電圧降下(電圧変動率)ε[p.u.]=Z[p.u.]*Q[p.u.]として記載があったので、根拠を見てみたところ以下の様になっていました。
抵抗を無視するので Vr=Vs-XQ/Vr
両辺をVrで割ると
Vr[p.u.]=Vs[p.u.]-XQ/Vr^2
ここで短絡容量Ps=Vr^2/Xであり、さらにPs=100/%X*Pbなので、上式に代入すると
Vr[p.u.]=Vs[p.u.]-Q/Ps
=Vs[p.u.]-%X/100*Q/Pb
=Vs [p.u.]-X[p.u.]Q[p.u.]
とのことでした。
皆さんのレスのお陰もあり、考え方の理解が深められたと思います。ありがとうございました。
まだまだ力不足ですが、二次試験まで頑張ろうと思います。またご指導よろしくお願いします。

Re: 2010電気計算9月号　2種2次変電 - fukusima

2010/09/26 (Sun) 19:53:31
*.bbtec.net

マサさま、こんばんは！！

質問させて下さい。
『抵抗を無視するので Vr=Vs-XQ/Vr　
　両辺をVrで割ると
　Vr[p.u.]=Vs[p.u.]-XQ/Vr^2』
上の『　』では
Vs[p.u.]＝Vs/Vr　と成ってますが･････これは成り立ちますか？
宜しく願います。

Re: 2010電気計算9月号　2種2次変電 - ﾏｻ

2010/09/26 (Sun) 21:15:15
*.spmode.ne.jp

fukusimaさん、こんばんわ！

[両辺をVrで割ると]の部分ですが、ご指摘の通り成り立ちませんね...テキストを覚えて記載したつもりでしたが、私の記憶違いかもしれません、すみません。
改めて考えると、この部分は、単位法にすると、が正しい様に思います。Vs,Vrはそれぞれ定格電圧で割り[p.u.]に、右辺第2項はVr基準での電圧降下なのでVrで割る事で[p.u.]になると思います。如何でしょうか？間違っていればご指導お願いします。