Re: 電験二種勉強方法 - 素敵なおじさん

2011/12/04 (Sun) 22:10:09
*.dti.ne.jp

例えば今年の二種の問題を解くために必要な数学の知識は、自動制御を除けば高校の数学の教科書が理解できるレベルで十分な気がします。
（数学といっても大部分が三角関数です）

その理由として、与えられた条件で式をたて、計算ができれば良いわけす。
計算の過程は数学の証明風に記述しても良いし、あるいは文学的に小説風な解説を書いても解答の数値があっていれば点がもらえます。
従って、数学の扱いとしては②の「理論の進捗に合わせて解答に必要な数学の知識を確かめる」が効率的だと考えます。

今年の二種二次のスコット変圧器の問題では巻数比と利用率の計算値が要求されていますが、解答例を見ればやはり数学の知識は高校レベルで十分なことが判ると思います。
この問題を少しひねって、「スコット変圧器の負荷が平衡している場合に電源側の三相が平衡していることを証明せよ」
という問題になると、数学的な証明問題の実力が問われることでしょう。

Re: 電験二種勉強方法 - KK

2011/12/04 (Sun) 22:54:25
*.ocn.ne.jp

私も②の方法に一票。
電験で必要な数学のみを、必要最小限勉強するほうが効率的です。
あまり数学に注力しても、解けない問題が逆に増えることにも
なりかねませんので。

Re: 電験二種勉強方法 - 鹿の骨

2011/12/05 (Mon) 18:51:49
*.dti.ne.jp

人によってやり方は色々ですが、電験二種数学さんは数学の基礎学力が無さ過ぎます。
電験二種と言ってもそんなに高等な数学を必要としません。
ガウス平面と初等の微分積分と三角関数が出来れば充分です。
普通科高等学校の数学で結構ですから一度キチンと勉強すべきです。
目標として1～2ヶ月でマスターする程度を狙って下さい。
半年以上かけてどうこうするものではありません。

尚、参考書によっては必要以上に難解な解説を載せているものが有ります。
オーム社にその傾向が顕著な感想をもっています。
簡単に説明出来るものをわざわざ難しく書いて何か凄いことを書いているように錯覚に陥っている様です。
参考書は最低でも２冊以上の併読が原則です。

Re: 電験二種勉強方法 - 素敵なおじさん

2011/12/05 (Mon) 22:18:22
*.dti.ne.jp

鹿は複素平面と書けば良いものを、ガウス平面などと知ったかぶりをするから素人は訳がわからなくなるのだな

複素数を表現するのに実軸（ｘ）と虚軸（ｊｙ）を直行座標系としてあらわしたり、ベクトルの長さと角度であらわしたりするごく一般的な複素数の表現方法のことを気取ってガウス平面などと書いたものだから心配することは無い。

複素数といっても２次元を超えるとかなり難解になる。
ｎ次元のｎ次ベクトルが全て直行するとき、なんてのは電験の計算には不要だから気にしなくてよいのだ

Re: 電験二種勉強方法 - 鹿の骨

2011/12/05 (Mon) 22:32:08
*.dti.ne.jp

案の定馬鹿が馬鹿記事を書く。

>鹿は複素平面と書けば良いものを、ガウス平面などと知ったかぶりをするから素人は訳がわからなくなるのだな

この素敵じゃない「素敵なおじさん」と言う御仁は電気関係の免許を一つも持っていない度素人。
素人の発言は無視が吉です。



>複素数を表現するのに実軸（ｘ）と虚軸（ｊｙ）を直行座標系としてあらわしたり、

↑此処までは正しい。

>ベクトルの長さと角度であらわしたりするごく一般的な複素数の表現方法のことを気取ってガウス平面などと書いたものだから心配することは無い。

↑これは「極座標」と言う。
間違ってもガウス平面では無いので注意。
度素人はこの様にデタラメを平気で書くので記事の内容を鵜呑みにしてはイケマセン・・・

Re: 電験二種勉強方法 - 電験二種数学

2011/12/06 (Tue) 06:05:29
*.emobile.ad.jp

皆さんアドバイスありがとうございます。参考になります。ガウス平面の所でつまずいています。三種は公式暗記で受かったのですが・・・。三種からステップアップで二種の勉強をさせている方で石橋 千尋先生の「いちばんよくわかる電験第2種数学入門帖」という書籍をお使いの方おりましたらどのようにお使いになっているかご教授ください。

Re: 電験二種勉強方法 - すてきな鹿の骨おじさん

2011/12/06 (Tue) 09:49:31
*.ocn.ne.jp

「いちばんよくわかる電験第2種数学入門帖」はマンガがあり一見簡単なイメージがあるが一次用というより二次の入門用。一次受かっても二次問題がちんぷんかんのときしっかり基礎から勉強するのに向いている。

それいぜんに
３種受かりが２種一次理論でつまづいているのが不自然。

Re: 電験二種勉強方法 - 鹿の骨

2011/12/06 (Tue) 18:21:04
*.dti.ne.jp

>ガウス平面の所でつまずいています。
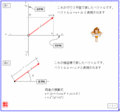
ガウス平面に関して解説を作っていたのですが参照先のサーバーが廃止になっていますので改めて貼ります。
1/10

Re: 電験二種勉強方法 - 鹿の骨

2011/12/06 (Tue) 18:22:07
*.dti.ne.jp

２／１０

Re: 電験二種勉強方法 - 鹿の骨

2011/12/06 (Tue) 18:22:46
*.dti.ne.jp

３／１０

Re: 電験二種勉強方法 - 鹿の骨

2011/12/06 (Tue) 18:23:31
*.dti.ne.jp

４／１０

Re: 電験二種勉強方法 - 鹿の骨

2011/12/06 (Tue) 18:24:24
*.dti.ne.jp

５／１０

Re: 電験二種勉強方法 - 鹿の骨

2011/12/06 (Tue) 18:25:11
*.dti.ne.jp

６／１０

Re: 電験二種勉強方法 - 鹿の骨

2011/12/06 (Tue) 18:25:42
*.dti.ne.jp

７／１０

Re: 電験二種勉強方法 - 鹿の骨

2011/12/06 (Tue) 18:26:24
*.dti.ne.jp

８／１０

Re: 電験二種勉強方法 - 鹿の骨

2011/12/06 (Tue) 18:27:06
*.dti.ne.jp

９／１０

Re: 電験二種勉強方法 - 鹿の骨

2011/12/06 (Tue) 18:27:42
*.dti.ne.jp

１０／１０

Re: 電験二種勉強方法 - 素敵なおじさん

2011/12/09 (Fri) 08:56:20
*.dti.ne.jp

ガウス平面と曲座標形式は別のものであるかのような鹿の記述が見られるが、明らかな誤りは訂正するのが知識人の義務というものである
なお、正しい記述を鹿の横車で削除するなどという暴挙は管理人としての資質が疑われるから公序良俗に反するもの、あるいは掲示板の趣旨に全くそぐわないもので無い限りは安易に削除などしてはいけない
管理人の横暴が目に余るようだと
広島市中区小町4-33
の人事に相談するという奥の手も無いではない

さて、余談はさておき
ガウス平面というのは二つの実数であらわされる複素数を平面に配置して二次元的に見やすいようにしたものはご承知の通りである。
ここで二つの実数の表現を（Ｘ、Ｙ）の直交座標系とするか、あるいは（Ｒ、θ）の曲座標系を選ぶかは任意である

即ち、ガウス平面と曲座標は異なるという鹿の主張は明らかな誤りであることは自明
鹿は高校の数学の基本に立ち返って勉強しろ

折角、鹿でも解けそうな簡単な問題を作ってやったのに横暴な管理人が削除してしまったのは日本の科学技術の発展には残念なことである

Re: 電験二種勉強方法 - 鹿の骨

2011/12/09 (Fri) 19:49:12
*.dti.ne.jp

「素敵なおじさん」君は必死すぎて哀れだ。

「曲座標」って何？
「ﾏｶﾞﾘｻﾞﾋｮｳ」とでも読むのかな？
「極座標」も知らないで何を書いているのか？
曲がっているのは全く素敵じゃ無い「素敵なおじさん」君の根性だな。
この御仁の特技は他人の揚げ足を取るのに必死で自分の足を取ってひっくり返るというもの。
今回も見事にひっくり返っているが、この御仁は「恥」という言葉を知らないようだ。

Re: 電験二種勉強方法 - 鹿の骨

2011/12/10 (Sat) 16:35:05
*.dti.ne.jp

「曲がり座標」とかいう発明をされても困るので、ガウス平面と極座標の違いを書いておく。
簡単な話。
この程度は普通科高等学校の数学の授業で習う。
θはラジアンでも度（デグリー）でも良い。
これは重要な事。
エクスポーネンシャル関数で極座標を表す場合が有るが、ラジアン値しか使えないので使い勝手が悪くお勧めしない。

Re: 電験二種勉強方法 - 鹿の骨

2011/12/10 (Sat) 23:30:06
*.dti.ne.jp

参考までにガウス平面と極座標のグラフ用紙(擬き)をうｐします。
「素敵なおじさん」君には理解不能だと思いますが、これをご覧になった多くの方はご理解願えると思います。